반응형
1. 힙 이란?
힙은 완전 이진 트리 기반의 자료 구조로, 항상 최대값 또는 최솟값을 빠르게 찾을 수 있도록 구성된 트리이다.
최대 힙은 최대 값이 루트 노드로 오는 힙
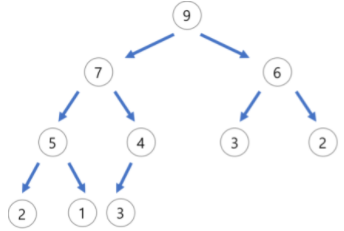
최소 힙은 최소 값이 루트 노드로 오는 힙
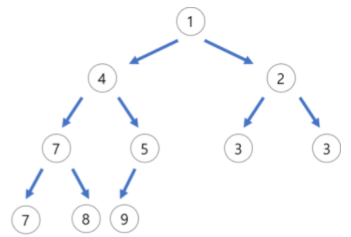
2. heapq - 내장 모듈
파이썬에서는 heapq 모듈을 임포트 해줌으로써 힙을 쉽게 다를 수 있다.
2-1. heapq.heappush(heap, item)
힙에 요소들을 추가하는 함수이다.
import heapq
heap = []
heapq.heappush(heap, 3)
heapq.heappush(heap, 1)
heapq.heappush(heap, 5)
print(heap) # 출력: [1, 3, 5] (최소 힙 유지)
2-2. heapq.heappop(heap)
힙에서 최소값을 제거하고 반환해주는 함수이다.
print(heap) # 출력: [1, 3, 5] 이라고 가정
print(heapq.heappop(heap)) # 출력: 1
print(heap) # 출력: [3, 5] (힙 속성 유지)
2-3. heapq.heappushpop(heap, item)
힙에서 최소값을 반환 후, 최솟값을 반환하는 함수이다.
print(heap) # 출력: [1, 3, 5] 이라고 가정
print(heapq.heapreplace(heap, 2)) # 최솟값(1) 제거 후 2 삽입
print(heap) # 출력: [2, 3, 5, 7]
2-4. heapq.heapify(heap)
리스트를 최소 힙으로 변경해주는 함수이다.
import heapq
arr = [5, 1, 8, 3]
heapq.heapify(arr) # 리스트를 최소 힙으로 변환
print(arr) # 출력: [1, 3, 8, 5] (힙 속성 유지)
2-5. 최대 힙
최대힙을 구현하기 위해서는 heap을 구성할때 음수로 변환해서 진행해주면 된다.
import heapq
max_heap = []
heapq.heappush(max_heap, -3) # 3을 음수로 변환하여 삽입
heapq.heappush(max_heap, -1) # 1을 음수로 변환하여 삽입
heapq.heappush(max_heap, -5) # 5을 음수로 변환하여 삽입
print(-heapq.heappop(max_heap)) # 5 (최댓값)
print(-heapq.heappop(max_heap)) # 3
print(-heapq.heappop(max_heap)) # 1
2-6. 가장 큰 값, 가장 작은 값을 리스트로 반환
힙이 아니라 리스트를 매개 변수로 넘겨줘야한다.
### 가장 큰 값 ###
import heapq
arr = [1, 3, 5, 7, 9, 2, 4, 6, 8]
print(heapq.nlargest(3, arr)) # 출력: [9, 8, 7]
students = [("Alice", 85), ("Bob", 92), ("Charlie", 88)]
print(heapq.nlargest(2, students, key=lambda x: x[1]))
# 출력: [('Bob', 92), ('Charlie', 88)] (점수 기준)
### 가장 작은 값 ###
import heapq
arr = [1, 3, 5, 7, 9, 2, 4, 6, 8]
print(heapq.nsmallest(3, arr)) # 출력: [1, 2, 3]
students = [("Alice", 85), ("Bob", 92), ("Charlie", 88)]
print(heapq.nsmallest(2, students, key=lambda x: x[1]))
# 출력: [('Alice', 85), ('Charlie', 88)] (점수 기준)
반응형
'Python > 알고리즘 - 이론' 카테고리의 다른 글
| [자료구조 멘토링] 유클리드 호제법을 이용한 최소 공배수, 최대 공약수 (feat.Python) (0) | 2025.02.24 |
|---|---|
| [자료구조 멘토링] 정렬 이론 (feat.Python) (0) | 2025.02.04 |
| [자료구조 멘토링] 트리 (feat.Python) (0) | 2025.02.04 |
| [자료구조 멘토링] 스택, 큐, 덱 (feat.Python) (0) | 2025.02.02 |
| [자료구조 멘토링] 시간 복잡도 (0) | 2025.01.20 |
